Cách vẽ điểm đối xứng trong tam giác
Lý thuyết đối xứng trục
1. Hai điểm đối xứng qua một đường thẳng
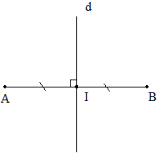
- Định nghĩa: Hai điểm gọi là đối xứng với nhau qua đường thẳng \(d\) nếu \( d\) là đường trung trực của đoạn thẳng nối hai điểm đó.
Ví dụ: Cho điểm B đối xứng với điểm A qua đường thẳng d thì d là đường trung trực của đoạn thẳng AB.
- Qui ước: Nếu điểm \(B\) nằm trên đường thẳng \(d\) thì điểm đối xứng với \(B\) qua đường thẳng \(d\) cũng là điểm \(B\).
2. Hai hình đối xứng qua một đường thẳng
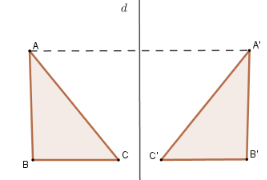
- Định nghĩa: Hai hình gọi là đối xứng với nhau qua đường thẳng \(d\) nếu mỗi điểm thuộc hình này đối xứng với một điểm thuộc hình kia qua đường thẳng \(d\) và ngược lại.
- Đường thẳng \(d\) gọi là trục đối xứng của hai hình đó.
3. Hình có trục đối xứng
Định nghĩa: Đường thẳng \(d\) gọi là trục đối xứng của hình \(H\) nếu điểm đối xứng với mỗi điểm thuộc hình \(H\) qua đường thẳng \(d\) cũng thuộc hình \(H.\)
Ta nói rằng hình \(H\) có trục đối xứng.
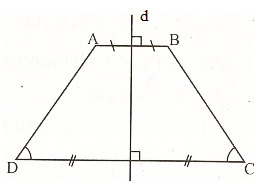
Định lí: Đường thẳng đi qua trung điểm hai đáy của hình thang cân là trục đối xứng của hình thang cân đó.
Trên hình vẽ, đường thẳng d là trục đối xứng của hình thang cân ABCD.
Loigiaihay.com
Bài tiếp theo
-
Trả lời câu hỏi 1 Bài 6 trang 84 SGK Toán 8 Tập 1
Trả lời câu hỏi 1 Bài 6 trang 84 SGK Toán 8 Tập 1. Cho đường thẳng d
-
Trả lời câu hỏi 2 Bài 6 trang 84 SGK Toán 8 Tập 1
Trả lời câu hỏi 2 Bài 6 trang 84 SGK Toán 8 Tập 1. Cho đường thẳng d và đoạn thẳng AB (h.51)...
-
Trả lời câu hỏi 3 Bài 6 trang 86 SGK Toán 8 Tập 1
Trả lời câu hỏi 3 Bài 6 trang 86 SGK Toán 8 Tập 1. Cho tam giác ABC cân tại A, đường cao AH (h.55).
-
Trả lời câu hỏi 4 Bài 6 trang 86 SGK Toán 8 Tập 1
Trả lời câu hỏi 4 Bài 6 trang 86 SGK Toán 8 Tập 1. Mỗi hình sau có bao nhiêu trục đối xứng?
-
Bài 35 trang 87 SGK Toán 8 tập 1
Giải bài 35 trang 87 SGK Toán 8 tập 1. Vẽ hình đối xứng với cá hình đã cho qua trục d (h.58).
- Lý thuyết đường trung bình của tam giác, của hình thang
- Lý thuyết Hình bình hành
- Lý thuyết hình thang cân
- Bài 67 trang 31 SGK Toán 8 tập 1
Lý thuyết đối xứng trục
1. Hai điểm đối xứng qua một đường thẳng
- Định nghĩa: Hai điểm gọi là đối xứng với nhau qua đường thẳng \(d\) nếu \( d\) là đường trung trực của đoạn thẳng nối hai điểm đó.
Ví dụ: Cho điểm B đối xứng với điểm A qua đường thẳng d thì d là đường trung trực của đoạn thẳng AB.
- Qui ước: Nếu điểm \(B\) nằm trên đường thẳng \(d\) thì điểm đối xứng với \(B\) qua đường thẳng \(d\) cũng là điểm \(B\).
2. Hai hình đối xứng qua một đường thẳng
- Định nghĩa: Hai hình gọi là đối xứng với nhau qua đường thẳng \(d\) nếu mỗi điểm thuộc hình này đối xứng với một điểm thuộc hình kia qua đường thẳng \(d\) và ngược lại.
- Đường thẳng \(d\) gọi là trục đối xứng của hai hình đó.
3. Hình có trục đối xứng
Định nghĩa: Đường thẳng \(d\) gọi là trục đối xứng của hình \(H\) nếu điểm đối xứng với mỗi điểm thuộc hình \(H\) qua đường thẳng \(d\) cũng thuộc hình \(H.\)
Ta nói rằng hình \(H\) có trục đối xứng.
Định lí: Đường thẳng đi qua trung điểm hai đáy của hình thang cân là trục đối xứng của hình thang cân đó.
Trên hình vẽ, đường thẳng d là trục đối xứng của hình thang cân ABCD.
Loigiaihay.com
Bài tiếp theo 
-
Trả lời câu hỏi 1 Bài 6 trang 84 SGK Toán 8 Tập 1
Trả lời câu hỏi 1 Bài 6 trang 84 SGK Toán 8 Tập 1. Cho đường thẳng d
-
Trả lời câu hỏi 2 Bài 6 trang 84 SGK Toán 8 Tập 1
Trả lời câu hỏi 2 Bài 6 trang 84 SGK Toán 8 Tập 1. Cho đường thẳng d và đoạn thẳng AB (h.51)...
-
Trả lời câu hỏi 3 Bài 6 trang 86 SGK Toán 8 Tập 1
Trả lời câu hỏi 3 Bài 6 trang 86 SGK Toán 8 Tập 1. Cho tam giác ABC cân tại A, đường cao AH (h.55).
-
Trả lời câu hỏi 4 Bài 6 trang 86 SGK Toán 8 Tập 1
Trả lời câu hỏi 4 Bài 6 trang 86 SGK Toán 8 Tập 1. Mỗi hình sau có bao nhiêu trục đối xứng?
-
Bài 35 trang 87 SGK Toán 8 tập 1
Giải bài 35 trang 87 SGK Toán 8 tập 1. Vẽ hình đối xứng với cá hình đã cho qua trục d (h.58).
- Lý thuyết đường trung bình của tam giác, của hình thang
- Lý thuyết Hình bình hành
- Lý thuyết hình thang cân
- Bài 67 trang 31 SGK Toán 8 tập 1