Cách Chứng minh 1 điểm cách đều 3 cạnh

Sao chép

I. Các kiến thức cần nhớ

1. Tính chất tia phân giác của một góc

2. Tính chất ba đường phân giác của tam giác

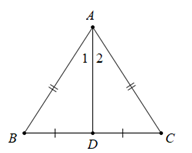
$\Delta ABC:$ $\left. \begin{array}{l}AB = AC\\\widehat {{A_1}} = \widehat {{A_2}}\end{array} \right\} \Rightarrow BD = DC$

Tam giác $ABC$ (hình vẽ) có ba đường phân giác giao nhau tại $I$. Khi đó

$\begin{array}{l}{\widehat A_1} = {\widehat A_2},{\widehat B_1} = {\widehat B_2},{\widehat C_1} = {\widehat C_2}.\\ID = IE = IF\end{array}$

II. Các dạng toán thường gặp

Dạng 1: Chứng minh hai đoạn thẳng bằng nhau, hai góc bằng nhau

Phương pháp:

Sử dụng các tính chất:

+ Ta sử dụng định lý: Điểm nằm trên tia phân giác của một góc thì cách đều hai cạnh của góc đó

$\left. \begin{array}{l}M \in Oz\\MA \bot Ox;MB \bot Oy\end{array} \right\} $$\Rightarrow MA = MB$

+ Giao điểm của hai đường phân giác của hai góc trong một tam giác nằm trên đường phân giác của góc thứ ba

+ Giao điểm các đường phân giác của tam giác cách đều ba cạnh của tam giác.

Dạng 2: Chứng minh hai góc bằng nhau

Phương pháp:

Ta sử dụng định lý: Điểm nằm bên trong một góc và cách đều hai cạnh của góc thì nằm trên tia phân giác của góc đó.

Dạng 3: Chứng minh tia phân giác của một góc

Phương pháp:

Ta sử dụng một trong các cách sau:

- Sử dụng định lý: Điểm nằm bên trong một góc và cách đều hai cạnh của góc thì nằm trên tia phân giác của góc đó.

- Sử dụng định nghĩa phân giác

- Chứng minh hai góc bằng nhau nhờ hai tam giác bằng nhau

Dạng 4: Bài toán về đường phân giác với các tam giác đặc biệt (tam giác cân, tam giác đều)

Phương pháp:

Ta sử dụng định lý: Trong một tam giác cân, đường phân giác của góc ở đỉnh đồng thời là đường trung tuyến của tam giác đó.

Dạng 5: Các dạng toán khác

Blog Hướng Dẫn Cách Là Gì ?